This MATLAB program simulates a full suspension mountain bike linkage. The simulation provides kinematics of all of the links including position, velocity, and acceleration. The simulation results show how the suspension will behave and how potential changes in the design will affect the suspension dynamics. The program makes use of algorithms for Jacobian matrix operations, vector loops to describe the kinematics of linkages, and programming a Newton-Rhapson algorithm to determine solutions to non-linear systems of equations.

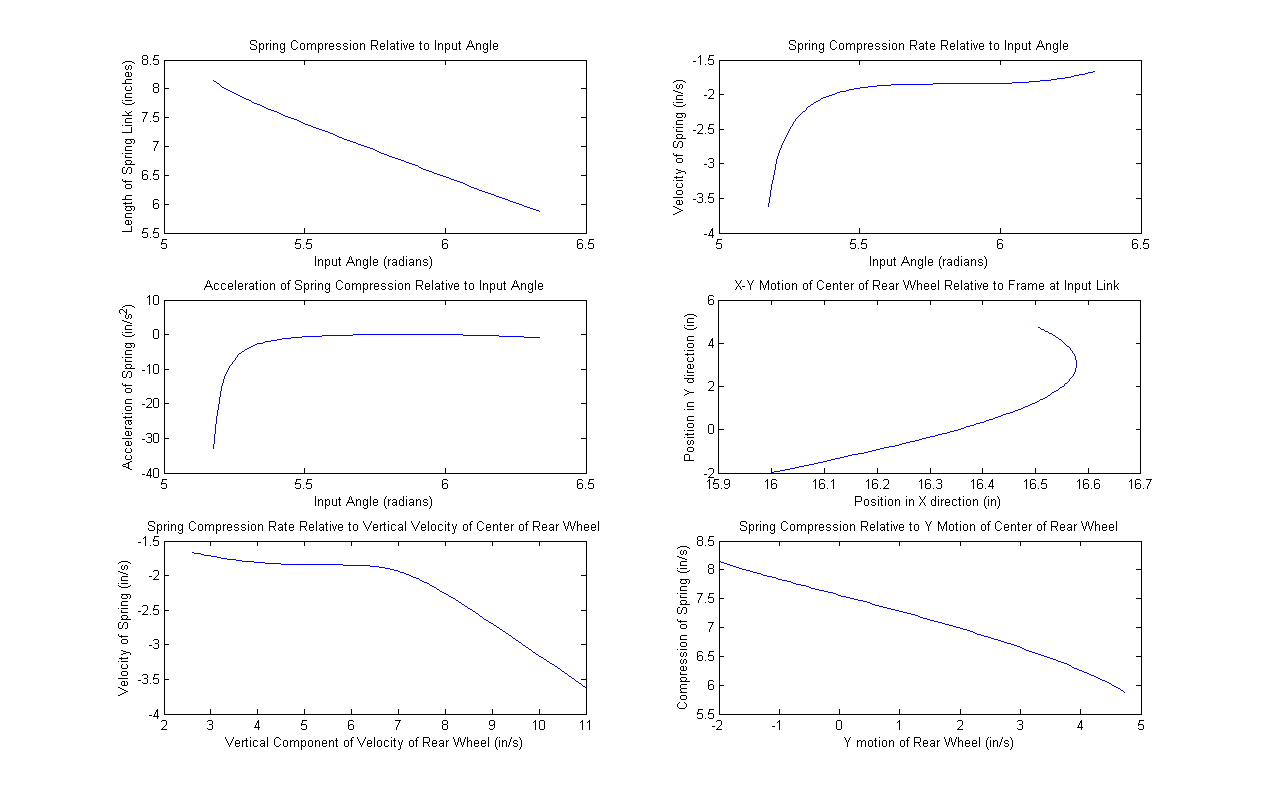
Results are shown for a full suspension mountain bike through its full range of travel.

The first step in analyzing the VPP suspension design was to determine the geometry of the system. First, two vector loop equations were created from the links of the suspension. These vector loops were broken down into x and y components, leading to four position equations. The time derivates of these four position equations yields the four velocity and acceleration equations. Using trigonometry, the fixed lengths and angles of the suspension were calculated. After plugging the fixed geometries into the four position equations there are only four unknown variables left. Since there are four equations and four unknowns, the solution can be determined. However, this system of equations is non-linear so a Newton-Rhapson algorithm must be used. This algorithm makes an initial guess of the values of the unknowns and then calculates the next guess using the inverse Jacobian matrix of the four position equations multiplied by those four position equations. After a number of iterations, the initial guess converges very close to the true values of the unknowns. Now that all of the link angles and lengths are known, they are plugged into the four derived velocity equations. This leaves only four velocity unknowns. The same step is repeated for the acceleration equations to get the four acceleration unknowns. The math is done in MATLAB through matrix algebra, specifically, the inverse Jacobian matrix of the position equations multiplied by the four derived equations in a matrix excluding the unknown terms. This multiplication of matrices yields a third matrix of the solutions to the four unknowns.

• 

  Figure 1

  Mountain Bike Suspension Motion

  Plots of mountain bike suspension simulation results.

MATLAB Source - mountain-bike-suspension.m