This program is a thermal Finite Element Analysis (FEA) solver for steady state heat transfer across 2D plates. The program numerically solves the steady state conduction problem using the Finite Difference Method. After the results are calculated, the program displays a color contour plot of the temperature of the plate after a given time interval.

Results are shown for a 2D fin with specified boundry conditions.

The model assumes 2D conduction with constant properties throughout the simulation. The model takes advantage of the vertical line of thermal symmetry at x = 0.020 m by adding an adiabatic boundary condition along the line of symmetry. The model assumes a specified convection boundary condition on x = 0 and y = Ly. The model assumes constant temperature boundary condition along the fin base.

• 

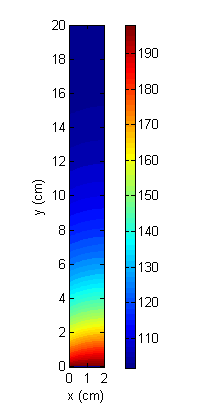
  Figure 1

  Steady State Temperature Across Fin

  Contour plot of fin temperature (deg C) for 2D steady-state conduction with Lx = 0.020 m, Ly = 0.200 m, Nx = 20, Ny = 200, fin base at 200 deg C, ambient air at 100 deg C, h = 500 W/m2K, and k = 50 W/mK.

MATLAB Source - steady-state-conduction-finite-differences.m