This MATLAB program simulates the trajectory of a rocket given initial conditions and phyiscal properties of the rocket. Numerical analysis is used to simulate the flight path of the rocket, including the effects of thrust, drag, mass change, and gravity.

Results are shown for a multi-stage rocket with variable mass, thrust, and drag.

The drag coefficient of the rocket, Equation 1, is used as an input to the dynamics model. The drag force of the rocket is then calculated using Equation 2.

\begin{equation} c_d = {F_d \over {{1 \over 2} \rho v^2 A}} \end{equation}
\begin{equation} F_d = {{1 \over 2} \rho v^2 c_d A} \end{equation}

• 

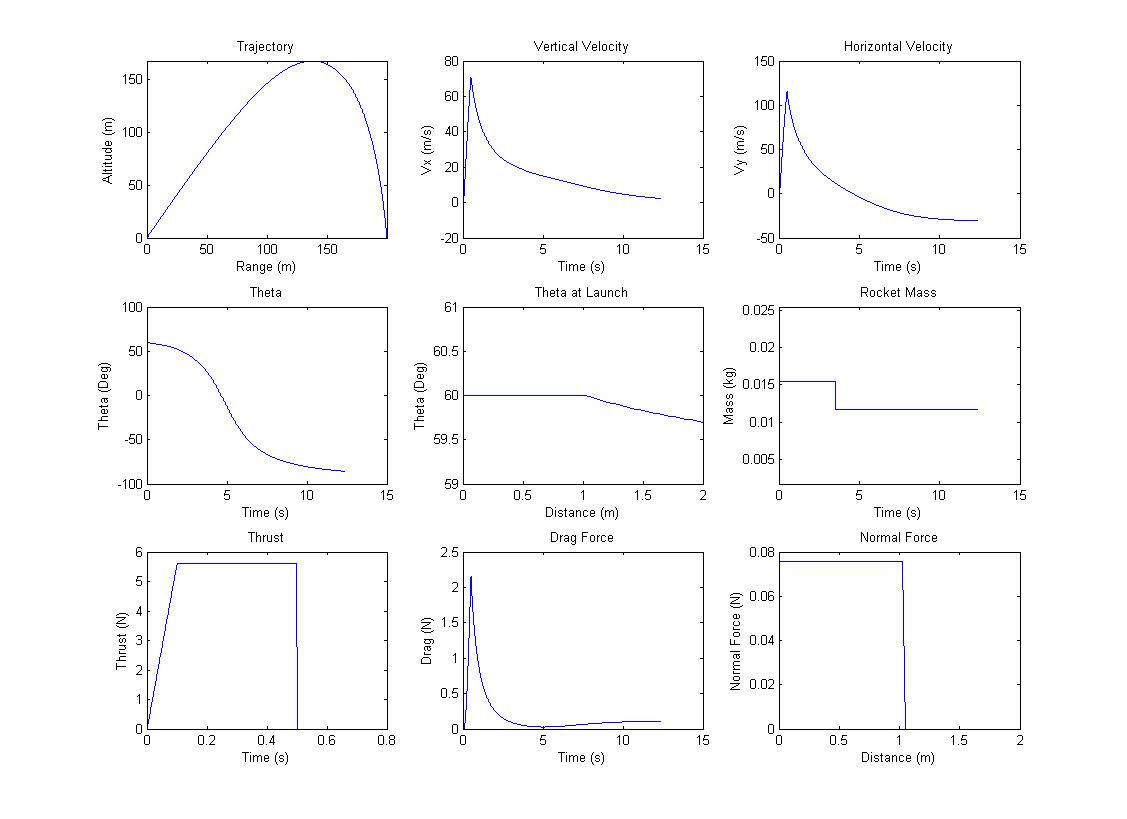
  Figure 1

  Rocket Trajectory Results

  Plots of rocket trajectory simulation results.

MATLAB Source - rocket-trajectory-simulation.m