Mental Math

Cube Roots

There is a simple process that allows someone to calculate the cube root of any integer number from 0^3 to 99^3 relatively quickly in their head. To find the integer cube root of a number up to 6 digits (0^3 to 99^3) in your head, memorize the cubes of the integers 1 through 9 shown in the table and follow the steps below.


Process:

1) The tens digit of the cube root answer can be determined by truncating the last 3 numbers off the given cube and seeing where it falls within the memorized table. The tens digit of the answer is the number corresonding to cube that is just smaller than the given truncated cube.

2) The ones digit can be found by taking the last digit of the given cube and finding the cube of that digit, by using the same memorized table. The last digit of this new cube is the ones digit of the cube root answer.


Example: What is the cube root of 389,017?

1) 390,017 -> 390 (With the last three digits truncated) -> 390 falls between 7^3(=343) and 8^3(=512). Therefore tens digit of the cube root answer is 7.

2) The last digit of the given cube is 7 -> 7^3 = 343 -> The last digit of 343 is 3. Therefore the ones digit of the cube root answer is 3.

The final answer is 73 and the cube root of 389,017 is in fact, 73.


Table to Memorize
Integer Cube
1 1
2 8
3 27
4 64
5 125
6 216
7 343
8 512
9 729
10 1000
Estimates

Quick Freefall Distance Estimates

An observer can estimate the height of a cliff by dropping a rock from the top of the cliff. The distance travelled by a free falling projectile follows the equation \(d=v_i+0.5at^2\). By applying the equation to a rock tossed from the top of a cliff with no vertical velocity component, the height of the cliff can be determined. In this scenario the distance to the bottom is \(0.5at^2\) where \(t\) is the time it takes for the rock to hit bottom and \(g\) is the gravitational acceleration \(32.174 ft/s^2\). By rounding the numbers it can be shown that the distance in feet is approximately \(16t^2\) where \(t\) is in seconds. A relatively quick way to estimate the distance in ones head is to take \(t^2\) times 10 and then add half of that number to itself. Comparisons of this approximatation method to the actual calculated distance are shown in the table below. This approximation underestimates the distance by about 7%, but manually timing the rocks free fall time is still probably a larger source of error.

\begin{equation} d=v_i+0.5at^2 \end{equation} \begin{equation} d=0.5at^2 \end{equation} \begin{equation} d=0.5*32t^2 \end{equation} \begin{equation} d=16t^2 \end{equation} \begin{equation} d=1.5*10t^2 \end{equation}

Free Fall Time (s) Distance (ft) Approximate Distance (ft)
1 16 15
2 64 60
3 145 135
4 258 240
5 403 375
6 580 540
7 789 735
8 1030 960
9 1304 1215
10 1610 1500
Estimates

Speed of Sound Estimate

The speed of sound in air at sea level is 340.29 m/s or 0.21 miles/s. It is generally easier to remember that sound travels approximately 1 mile in 5 seconds with 5% error.

Statistics

Useful Statistics Formulas

  • Combinations (Groups - Order does not matter)

  • Number of ways "n" things can be ordered
  • Answer:
    • \begin{equation} x = n! \end{equation}
  • Number of way "n" things can be ordered if taking "r" at a time and order in the pair is not imporant (a,b)=(b,a)
  • Answer:
    • \begin{equation} x = {n!\over {(n-r)!r!}} \end{equation}
  • Example:
  • The amount of unique number pairs in the set {1,2,3,4}, where order doesn't matter (1,2) = (2,1)
  • For pairs of two:
    • \begin{equation} r = 2 \end{equation}
  • With four items:
    • \begin{equation} n = 4 \end{equation}
  • Answer:
    • \begin{equation} x = {4!\over {(4-2)!2!}} = 6 \end{equation}

  • Permutations (Lists - Order does matter)

  • Number of way "n" things can be ordered if taking "r" at a time and order in each pair is imporant (a,b) != (b,a)
  • Answer:
    • \begin{equation} x = {n!\over {(n-r)!}} \end{equation}
Estimates

Stereoscopic Distance Estimates

An observer can estimate roughly how far away an object is if the approximate size of the object, or another near by object, is known. The ratio of a typical persons arm length to the distance between their eyes is about 10. Using this information and trigonemetry the distance to the referenced object can be estimated. First, the observer holds up their thumb and aligns it with the center of the referenced object with one eye closed. The observer then alternates between closing one eye and then the other such that only one eye is open at a time. The observer then estimates the distance the referenced object appears to jump back and forth. The estimated distance to the object is 10x this number.


Example:

If an observer looks off in the distance and sees a person and appears to be about 6 ft tall. The obsever then lines up their thumb over their view of the person with on eye closed. Then by alternating one closed then the other, they see that the referenced person moves back and forth about 12 ft (Using the person's 6ft height as reference for what 12 ft looks like at that distance. In this example, the distance from the observer to the person would be about 10x the percieved back and forth movement, or about 120 ft away.

Estimates

The Solar System to Scale

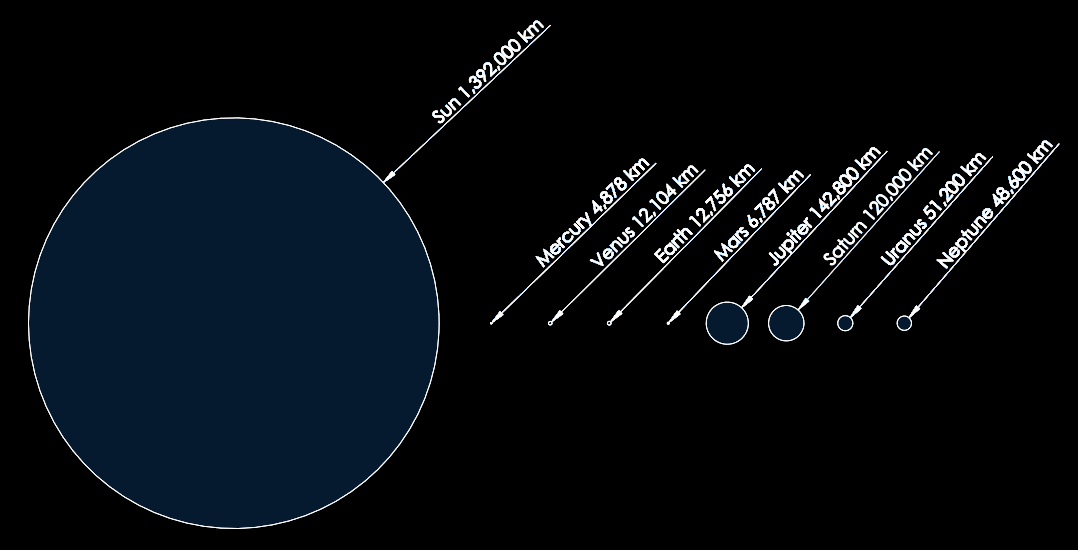
The solar system is commonly illustrated with pictures that show the planet sizes to scale, but the distances between them are not to scale or not to the same scale at least. A typical image, shown here, shows the planet sizes to scale, but the distances between them are not to scale. The video here illustrates the reason why the solar system is commonly shown this way, but this technique leads the audiance to beleive that the planets are relatively closer together than they actually are./p>

  • #
    Figure 1
    Planet Sizes

    Planet sizes to scale, but distances are not to scale.

The video here shows the planet sizes, starting with the Sun, and distances between them drawn to the same scale. When the video zooms out at the end, to show the entire solar system, some planets are smaller than a single pixel when depicted on a typical monitor.