This program is a thermal Finite Element Analysis (FEA) solver for transient heat transfer across 2D plates. The program numerically solves the transient conduction problem using the Finite Difference Method. The program displays a color contour plot of the temperature of the plate for each time step.

Results are shown for a square 2D plate with specified boundry conditions.

The model assumes transient 2D conduction with constant properties throughout the simulation. A stable time step must be set by taking into account the physical time constant. Selecting unstable time steps may lead to inconsistent results.

• 

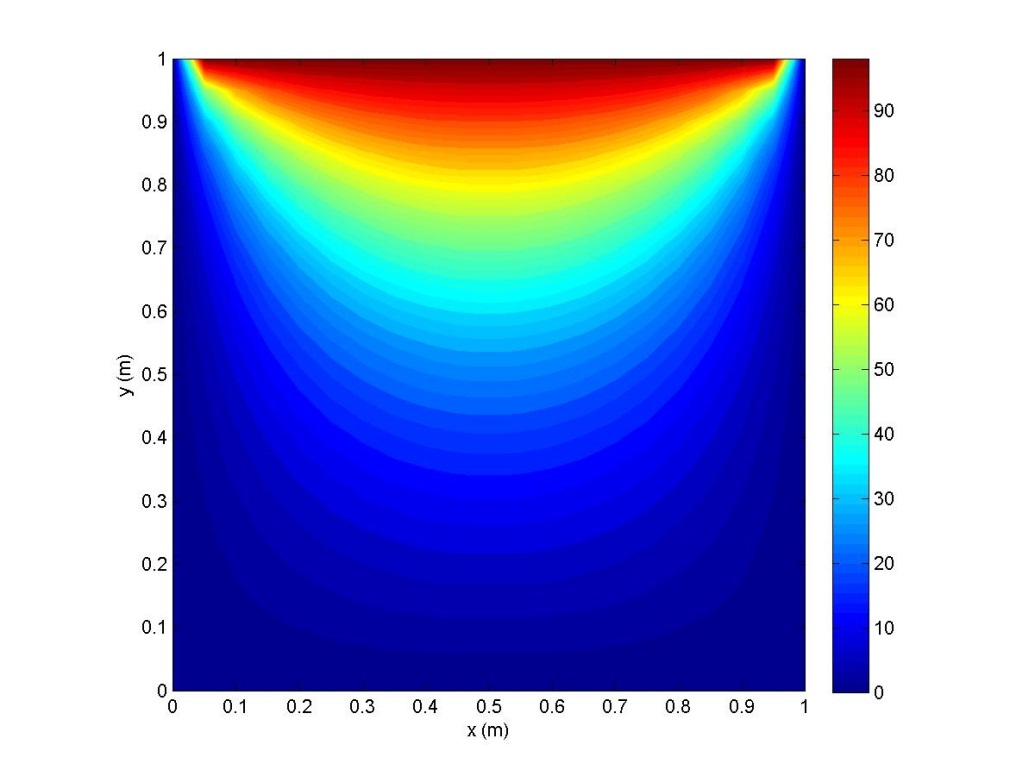
  Figure 1

  Transient Conduction

  Contour plot of temperature (deg C) for 2D, transient, constant property conduction with Lx = Ly = 1m, Nx = Ny = 20, and stable time step of 1000 seconds after a time of 184.44 hours.

• 

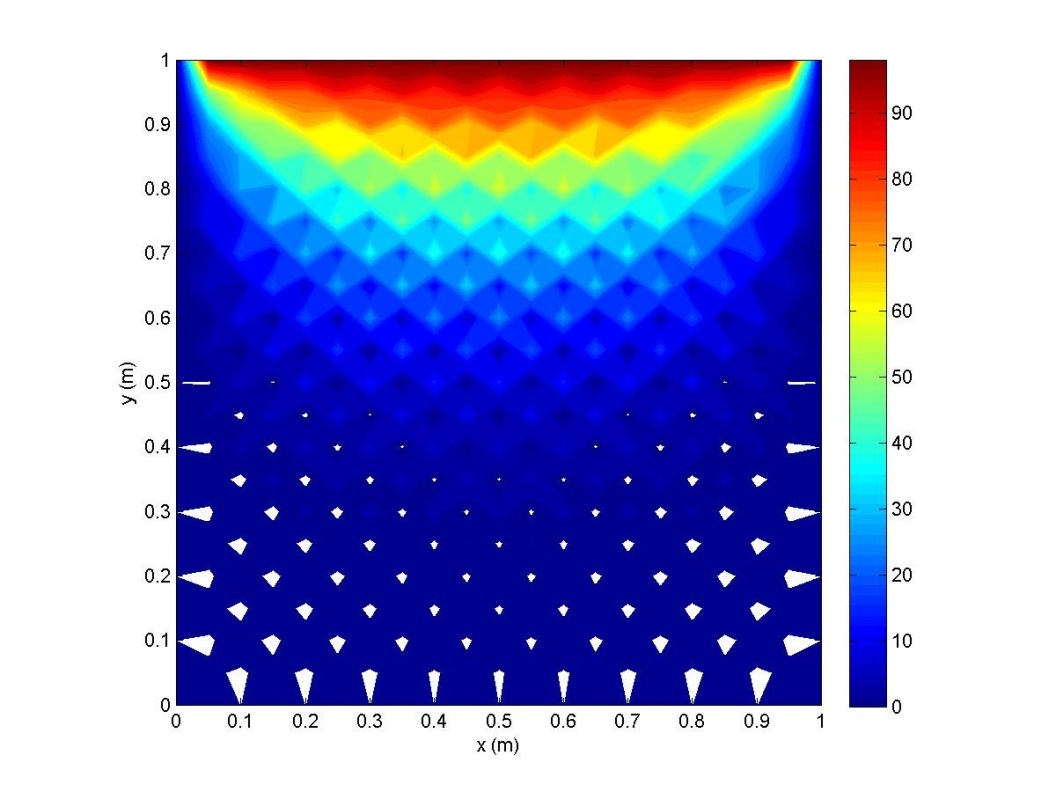
  Figure 2

  Transient Conduction, Unstable Start

  Contour plot of temperature (deg C) for 2D, transient, constant property conduction with Lx = Ly = 1m, Nx = Ny = 20, and unstable time step of 1500 seconds after a time of 27.08 hours.

• 

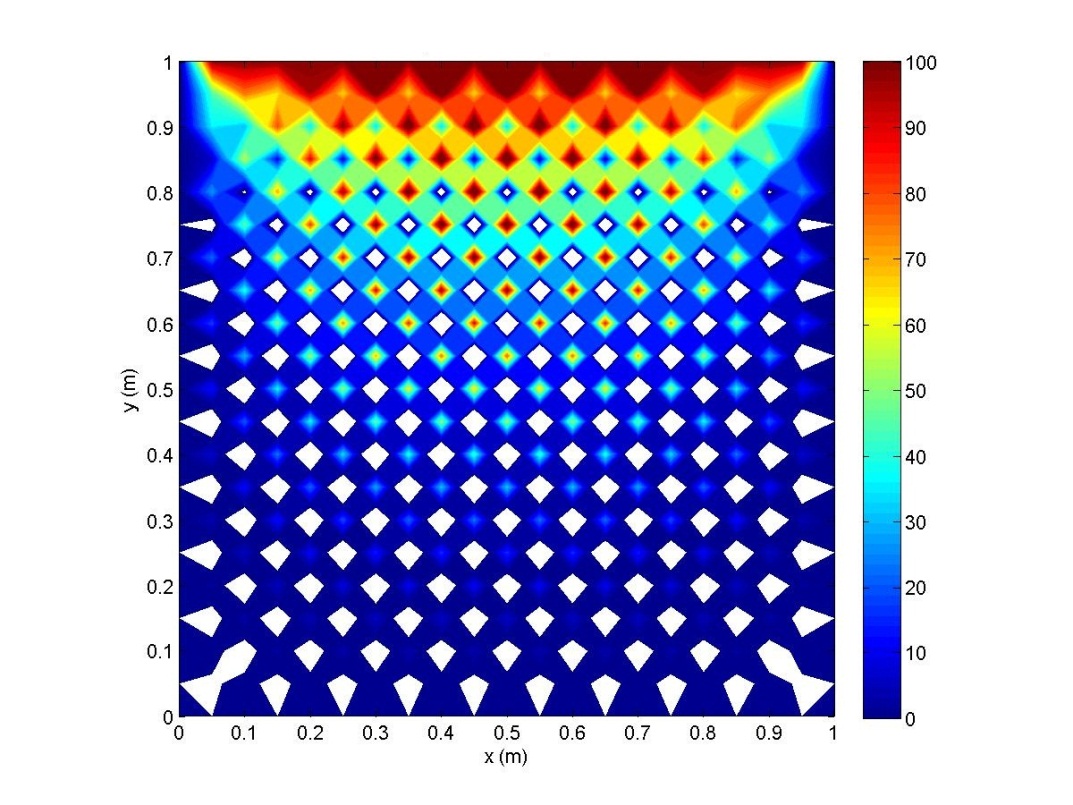
  Figure 3

  Transient Conduction, Unstable Progression

  Contour plot of temperature (deg C) for 2D, transient, constant property conduction with Lx = Ly = 1m, Nx = Ny = 20, and unstable time step of 1500 seconds after a time of 33.33 hours.

MATLAB Source - transient-conduction-finite-differences.m